PART I: THE PAPAYA PROBLEM
Dora and Boots, enjoying their stroll down Hustleberry Lane, notice a rustle in the bushes.
At 4:27 p.m., Swiper attacks Dora, steals their papayas from Dora's backpack, and tries to escape, but Dora yells “Swiper, no swiping!” which prevented Swiper from stealing their papayas. Swiper didn't want to admit defeat and thinks that if he can't have the papayas, then no one can. So he throws the papayas into a nearby geyser and scurries off. Both Dora and Boots lay motionless on the grass as they were too astonished from what had just happened. Their papayas are gone!
Boots stands up and stares into the geyser. He felt the ground shake beneath his feet. Then, a column of hot water shoots out of the geyser! Atop the column of water were the papayas, but the sight of the papayas didn't last long. The column of water disappears from Boots' sight, and the papayas fall back into the geyser. Boots looks at his watch and notes that it is now 4:30 p.m.
Boots, an expert on the subject of geysers, knows that geysers shoot their column of water at regular intervals, which would look like a sinusoidal pattern if the pattern were to be graphed. By studying the environment around him, he finds that the geyser—the one that Swiper threw the papayas in—only shoots out its column of water when the underground water reaches its maximum temperature of 119.7 degrees Celsius, while the coldest temperature the underground water can reach is -8.1 degrees Celsius at 4:30 a.m.
Boots wants to collect data related to the geyser, so he made questions for you to solve. Help Boots answer the questions, so that Dora and Boots know when to get ready to collect their papayas the next time the geyser shoots its column of water.
QUESTIONS
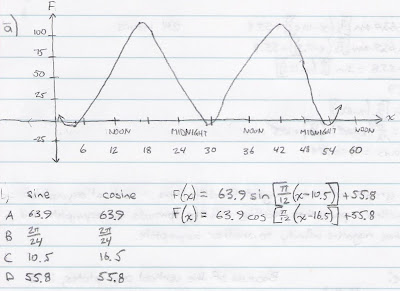
a) Sketch the graph, and express the graph as a sine and cosine function.
Image 1.1
We sketch a graph, labeling the x-axis as time (hours) and the y-axis as temperature (degrees Celsius). We will use 12:00 midnight of the day the papayas were stolen as our reference point, zero, on the x-axis.
The first time Dora and Boots witnessed the column of water shoot out of the geyser was at 4:30 PM (12 + 4.5 = 16.5 hours after midnight of the same day). At that point in time, the temperature of the water is at its maximum at 119.7 degrees Celsius. Also, at 4:30 AM (4.5 hours after midnight of the same day), the temperature of the water is at its minimum at -8.1 degrees Celsius. These two pieces of data are two of the coordinates of the maximum and minimum points on the graph, with the coordinates being (16.5, 119.7) and (4.5, -8.1), respectively.
All sine and cosine functions can be expressed as...
f(x) = AsinB(x-C)+D and f(x) = AcosB(x-C)+D,
respectively, whereas...
- parameter A is the amplitude (the distance of the maximum and minimum values from the sinusoidal axis);
- parameter B determines the period according to the relation "period=2pi/B";
- parameter C is the phase shift (the horizontal shift); and
- parameter D is the vertical shift (determines the sinusoidal axis).
D is the vertical shift, which determines the sinusoidal axis. It is the change in distance from one point of a basic function (where the function has D = 0) to a function that has undergone a translation of D units down or up. D can be found by taking the average of the maximum and minimum values of the function.
D = [119.7 + (-8.1)] / 2 = 55.8
A is the amplitude, which determines the distance of the maximum and minimum values of the "geyser function" from the sinusoidal axis. A can be found by subtracting the value of the sinusoidal axis from the maximum value, or A can be found by adding the value of the sinusoidal axis to the minimum value.
A = 119.7 - 55.8 = 63.9 OR
A = -8.1 + 55.8 = 63.9
B determines the period according to the relation "period=2pi/B". The period is the distance between two consecutive points on a wave; it is the horizontal distance along the x-axis required to make one "wave."
Since the time of the maximum value is 16.5 and the time of the minimum value is 4.5, the time it takes for the water to change from the coldest temperature (the minimum value) to the hottest temperature (the maximum value) is 12 hours (16.5 - 4.5 = 12). This, so far, makes up half the period. For the hottest temperature to return to the coldest temperature, that would take another 12 hours. The period, in this case, would be 24 hours.
period = 2pi/B
B = 2pi/period
B = 2pi/24
B = pi/12
C is the phase shift, which is also known as the horizontal shift. It is the change in distance from one point of a basic function (where the function has C = 0) to a function that has undergone a translation of C units to the left or right.
When referring to the basic cosine function, the maximum value of the "geyser function" closest to the y-axis is translated 16.5 units to the right; C = 16.5. When referring to the basic sine function, the mid-value between the maximum and the minimum time values of the "geyser function" is translated 10.5 units to the right; C = 10.5. Remember, there are an infinite number of equations that can be derived from this function, so the equations that we generated, found in Image 1.1, are only two of the infinite possible equations of this function.
b) Dora predicts the temperature of the water will be the same at 8:30 AM and at 8:30 PM. Is her prediction true?
Image 1.2

8:30 AM is 8.5 hours after 12 midnight. We have an equation that can determine the temperature or the time of any point on the "geyser function." Plug in the 8.5 hours as x, and we get 23.85 degrees Celsius. Similarly, 8:30 PM is 8.5 hours after 12 noon (12 + 8.5 = 20.5). Plug in the 20.5 hours as x, and we get 87.75 degrees Celsius. Therefore, Dora's prediction is wrong.
c) The boiling point of water is 100 degrees Celsius. Algebraically determine how many hours the water will maintain a temperature of 100 degrees Celsius or hotter.
Image 1.3
6.1646 hours = 6 hours 9.876 minutes = 6 hours 9 minutes 53 seconds (rounded to the nearest second)
Note that 13.4177 and 19.5823 aren't the only answers this equation can give us. Because the sinusoidal function has a domain of (negative infinity, positive infinity), then the time periods of when the water is as hot as 100 degrees Celsius is at 13.4177 + 2kpi and 19.5823 + 2kpi, where k is an integer and rounded to four decimal places.
d) Algebraically determine at what time the column of water will shoot out of the geyser. How long will Dora and Boots have to wait for their papayas to shoot out of the geyser?
Image 1.4

We know that the column of water will shoot out of the geyser when the underground water reaches its maximum temperature of 119.7 degrees Celsius. We have the temperature. We have the equation. Plug the 119.7 as f(x) into the equation to give us 16.5 hours after midnight. 16.5 hours is 4:30 PM. This means that Dora and Boots will have to wait until 4:30 PM, the next day, to get their papayas back; that is 24 hours.
e) Can the sinusoidal pattern of the graph of the geyser's column of water ever be expressed as a tangent function? Explain.
Image 1.5
f) If a natural catastrophic event occurs and disrupts the usual graph of the function of the geyser's column of water, f(x), in such a way that the "geyser function" would undergo a vertical stretch of 3, a reflection over the x-axis, a horizontal compression of 0.5, a translation of 4 units to the right, and then an upward translation of 3 units, then what would the new equation of the function be?
Any given function can be expressed as...
y = af([b(x-c)]+d
whereas...
- parameter a is the vertical stretch/compression of a function; the y-coordinates of f(x) are multiplied by a;
- parameter b is the horizontal stretch/compression of a function; the x-coordinates of f(x) are multiplied by 1/b;
- parameter c is the horizontal shift; and
- parameter d is the vertical shift.
horizontal compression of 0.5 (B = 2)
translation of 4 units to the right (C = 4)
translation of 3 units upwards (D = 3)
Image 1.6



No comments:
Post a Comment