Reflection of the Episode (DEV)

Why did you choose the concepts you did to create your problem set?

As a group we decided to create questions that involved the concepts that were difficult for other students as well as for ourselves. We figured why should we work on questions that everybody was comfortable with. We should help others as well as ourselves with the questions. From information that we received from other people throughout the semester combinatorics, probability, conics, and circular functions were the most troublesome out of the other units. So we decided to focus on those concepts.

How do these problems provide an overview of your best mathematical understanding of what you have learned so far?

The questions that we created were a bit troublesome for some of our fellow students. So we decided to merge all of our understanding of those concepts to fully create and answer the problems. Working together allowed us to learn from each other and fully understand the concepts. That gave us a better understanding of the unit because we were able to teach each other about the unit. The questions provided us a way to combine the stuff that we learned throughout the course. As a group these questions were a challenge to create. The mathematical understanding that was put into creating the questions were quite valuable towards answering and describing the steps of getting the answers.

Did you learn anything from this assignment? Was it educationally valuable to you? (Be honest with this. If you got nothing out of this assignment then say that, but be specific about what you didn't like and offer a suggestion to improve it in the future.)

From this assignment we learned and gained some valuable information. We worked as a team to come up with challenging questions that we believed were helpful to fellow students as well as us. We learned from each other. What we noticed was that all of us had different specialties in the course. So we used that to our advantage. We taught each other what we knew. So we actually learned from each other and used that knowledge to create those questions. What we got from this project was partly skills like time management, distribution of work, and teamwork all together. We used what we had to an advantage. Educationally, this project was very valuable. We were able to have some closure on the units that we covered. This Developing Expert Voices (DEV) project allowed us to conclude what we learned and to use that knowledge to help others. This reflection section was also very useful. It also gave us a chance to tell others as well as expressing our thoughts toward what we had done throughout the course.

Introduction to Dora's Pre- Calculus Episode

The first question you are about to witness is an identity question. In identities algebraic expressions are manipulated in legitimate ways like multiplying by 1 or different forms of ones or using trigonometric identities without changing the value of the expression. We manipulate or how Mr.K calls it Algebraically Massage the expressions so we can prove that an algebraic expression is equal to the other one. There are tons of trigonometric identities and they are all derived from the basic identity sin²x + cos²x = 1. Feel free to pause or rewind the video to read the descriptions if necessary. Time for the movie!!!



The rest of the DEV is below...

Dora and her Precalculus Homework

| View | Upload your own

Dora and her Precalculus Homework

Dora: Boots gave me another one. He's not giving me a break.

| View | Upload your own

Dora and Her Game of Go Fish

Dora wanted to play a good game of Go Fish with her friends. So She decided to invite 5 of her other friends over: Boots the Monkey, Benny the Bull, Señor Toucan, Liza the Lizard, and her cousin Diego.

Dora: Hey guys, lets play on top of that stump over there.

Boots: I want to sit with you Dora!

Benny: Me too!

Diego: Dora might cheat, I won't sit beside her.

a) Oh no Dora and her friends have a problem. How many ways can Dora and her friends sit at the tree stump to play cards when Dora has to sit with Boots and Benny? In addition Diego doesn't want to sit with Dora.

So to first solve this problem, let's analyze this question a bit more. Since Dora must sit with Boots and Benny, how many ways can they sit together? They are consider a single object in this group which means that there are only 4 people that has to be arranged at the tree stump. We can then find the number of ways that those four people can sit at the round stump. Remember that Diego doesn't want to sit with Dora...

| View | Upload your own

b)
Dora: Okay, we've sorted this out. Now let's play some go fish.

Liza: I don't know how to play.

Benny: I do. In go fish, we all first have five cards, and the objective of this game is to get rid of our hands by making pairs. We can get pairs by drawing a card or asking if another player has the card you need. First one to lose all of the cards in their hand wins!

Liza: Wow that sound's easy enough, you are so smart Benny.

Benny: Why thank you...

Diego: Let's just play already. I'll deal.

So Diego give each player five cards. Boots got his 5 cards first. Him being a gambler and all wants to have a little fun.

Boots: Okay I'm going first and I bet I can win this by just picking up only one card.

Liza: Let's see you try Boots!.

Woah, Boots is being a bit gutsy. What is he going to do? What is the probability of Boots winning by drawing only one card if: i) No one has the card he needs ii) One person has the card he needs iii) Two people have the card he needs?

In order to solve this we have to find the probability of getting a 5 card Poker hand of 2 Pairs or a 4 of a Kind. Then we must solve the probability of getting that card that Boots needs to win.

| View | Upload your own

Boots: Woot I won in one draw. I told you I could win. Hahahaha!

Diego: Darn you Boots!!

Dora: Thank you guys for helping me with today's problems. What was you favorite part of today?...(silence)...me too!!!

Dora's Adventures I

PART I: THE PAPAYA PROBLEM

Dora and Boots, enjoying their stroll down Hustleberry Lane, notice a rustle in the bushes.

At 4:27 p.m., Swiper attacks Dora, steals their papayas from Dora's backpack, and tries to escape, but Dora yells “Swiper, no swiping!” which prevented Swiper from stealing their papayas. Swiper didn't want to admit defeat and thinks that if he can't have the papayas, then no one can. So he throws the papayas into a nearby geyser and scurries off. Both Dora and Boots lay motionless on the grass as they were too astonished from what had just happened. Their papayas are gone!

Boots stands up and stares into the geyser. He felt the ground shake beneath his feet. Then, a column of hot water shoots out of the geyser! Atop the column of water were the papayas, but the sight of the papayas didn't last long. The column of water disappears from Boots' sight, and the papayas fall back into the geyser. Boots looks at his watch and notes that it is now 4:30 p.m.

Boots, an expert on the subject of geysers, knows that geysers shoot their column of water at regular intervals, which would look like a sinusoidal pattern if the pattern were to be graphed. By studying the environment around him, he finds that the geyser—the one that Swiper threw the papayas in—only shoots out its column of water when the underground water reaches its maximum temperature of 119.7 degrees Celsius, while the coldest temperature the underground water can reach is -8.1 degrees Celsius at 4:30 a.m.

Boots wants to collect data related to the geyser, so he made questions for you to solve. Help Boots answer the questions, so that Dora and Boots know when to get ready to collect their papayas the next time the geyser shoots its column of water.

QUESTIONS

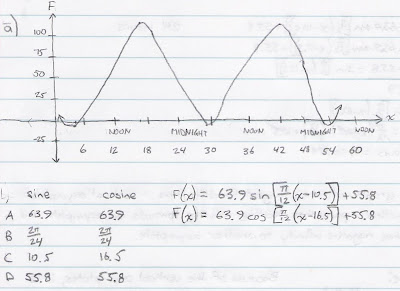
a) Sketch the graph, and express the graph as a sine and cosine function.

Image 1.1

We sketch a graph, labeling the x-axis as time (hours) and the y-axis as temperature (degrees Celsius). We will use 12:00 midnight of the day the papayas were stolen as our reference point, zero, on the x-axis.

The first time Dora and Boots witnessed the column of water shoot out of the geyser was at 4:30 PM (12 + 4.5 = 16.5 hours after midnight of the same day). At that point in time, the temperature of the water is at its maximum at 119.7 degrees Celsius. Also, at 4:30 AM (4.5 hours after midnight of the same day), the temperature of the water is at its minimum at -8.1 degrees Celsius. These two pieces of data are two of the coordinates of the maximum and minimum points on the graph, with the coordinates being (16.5, 119.7) and (4.5, -8.1), respectively.

All sine and cosine functions can be expressed as...

f(x) = AsinB(x-C)+D and f(x) = AcosB(x-C)+D,

respectively, whereas...

• parameter A is the amplitude (the distance of the maximum and minimum values from the sinusoidal axis);
  
• parameter B determines the period according to the relation "period=2pi/B";
  
• parameter C is the phase shift (the horizontal shift); and
  
• parameter D is the vertical shift (determines the sinusoidal axis).

D is the vertical shift, which determines the sinusoidal axis. It is the change in distance from one point of a basic function (where the function has D = 0) to a function that has undergone a translation of D units down or up. D can be found by taking the average of the maximum and minimum values of the function.
D = [119.7 + (-8.1)] / 2 = 55.8

A is the amplitude, which determines the distance of the maximum and minimum values of the "geyser function" from the sinusoidal axis. A can be found by subtracting the value of the sinusoidal axis from the maximum value, or A can be found by adding the value of the sinusoidal axis to the minimum value.
A = 119.7 - 55.8 = 63.9 OR
A = -8.1 + 55.8 = 63.9

B determines the period according to the relation "period=2pi/B". The period is the distance between two consecutive points on a wave; it is the horizontal distance along the x-axis required to make one "wave."

Since the time of the maximum value is 16.5 and the time of the minimum value is 4.5, the time it takes for the water to change from the coldest temperature (the minimum value) to the hottest temperature (the maximum value) is 12 hours (16.5 - 4.5 = 12). This, so far, makes up half the period. For the hottest temperature to return to the coldest temperature, that would take another 12 hours. The period, in this case, would be 24 hours.
period = 2pi/B
B = 2pi/period
B = 2pi/24
B = pi/12

C is the phase shift, which is also known as the horizontal shift. It is the change in distance from one point of a basic function (where the function has C = 0) to a function that has undergone a translation of C units to the left or right.

When referring to the basic cosine function, the maximum value of the "geyser function" closest to the y-axis is translated 16.5 units to the right; C = 16.5. When referring to the basic sine function, the mid-value between the maximum and the minimum time values of the "geyser function" is translated 10.5 units to the right; C = 10.5. Remember, there are an infinite number of equations that can be derived from this function, so the equations that we generated, found in Image 1.1, are only two of the infinite possible equations of this function.

b) Dora predicts the temperature of the water will be the same at 8:30 AM and at 8:30 PM. Is her prediction true?

Image 1.2

8:30 AM is 8.5 hours after 12 midnight. We have an equation that can determine the temperature or the time of any point on the "geyser function." Plug in the 8.5 hours as x, and we get 23.85 degrees Celsius. Similarly, 8:30 PM is 8.5 hours after 12 noon (12 + 8.5 = 20.5). Plug in the 20.5 hours as x, and we get 87.75 degrees Celsius. Therefore, Dora's prediction is wrong.

c) The boiling point of water is 100 degrees Celsius. Algebraically determine how many hours the water will maintain a temperature of 100 degrees Celsius or hotter.

Image 1.3

We have an equation that can determine the temperature or the time of any point on the "geyser function." Plug in 100 as F(x), and we get two answers: 13.4177 + 2kpi hours and 19.5823 + 2kpi hours, whereas k is an integer. Referring to the graph, we can see that these two answers mean that the temperature of when the water will be exactly 100 degrees Celsius is at 13.4177 hours after midnight and 19.5823 hours after midnight. Therefore, the time between 13.4177 hours and 19.5823 is the time period when the water is over 100 degrees Celsius. If we find the difference between 19.5823 and 13.4177, we find the total number of hours of when the water has a temperature at or above 100 degress Celsius in a given period; that is 6.1646 hours.

6.1646 hours = 6 hours 9.876 minutes = 6 hours 9 minutes 53 seconds (rounded to the nearest second)

Note that 13.4177 and 19.5823 aren't the only answers this equation can give us. Because the sinusoidal function has a domain of (negative infinity, positive infinity), then the time periods of when the water is as hot as 100 degrees Celsius is at 13.4177 + 2kpi and 19.5823 + 2kpi, where k is an integer and rounded to four decimal places.

d) Algebraically determine at what time the column of water will shoot out of the geyser. How long will Dora and Boots have to wait for their papayas to shoot out of the geyser?

Image 1.4

We know that the column of water will shoot out of the geyser when the underground water reaches its maximum temperature of 119.7 degrees Celsius. We have the temperature. We have the equation. Plug the 119.7 as f(x) into the equation to give us 16.5 hours after midnight. 16.5 hours is 4:30 PM. This means that Dora and Boots will have to wait until 4:30 PM, the next day, to get their papayas back; that is 24 hours.

e) Can the sinusoidal pattern of the graph of the geyser's column of water ever be expressed as a tangent function? Explain.

Image 1.5

f) If a natural catastrophic event occurs and disrupts the usual graph of the function of the geyser's column of water, f(x), in such a way that the "geyser function" would undergo a vertical stretch of 3, a reflection over the x-axis, a horizontal compression of 0.5, a translation of 4 units to the right, and then an upward translation of 3 units, then what would the new equation of the function be?

Any given function can be expressed as...

y = af([b(x-c)]+d

whereas...

• parameter a is the vertical stretch/compression of a function; the y-coordinates of f(x) are multiplied by a;
• parameter b is the horizontal stretch/compression of a function; the x-coordinates of f(x) are multiplied by 1/b;
• parameter c is the horizontal shift; and
  
• parameter d is the vertical shift.

vertical stretch of 3 and a reflection over the x-axis (A = -3)
horizontal compression of 0.5 (B = 2)
translation of 4 units to the right (C = 4)
translation of 3 units upwards (D = 3)

Image 1.6

Dora's Adventures II

PART II: THE ROYAL BRIDGE

Dora and Boots continue their journey along Hustleberry Lane until they notice a construction worker faced with a problem.

Construction Worker: Oh no. The Queen's Paddlewheel is journeying along this river, but the construction of the Royal Bridge isn't finished yet! I'm too tired and hungry to finish constructing the Royal Bridge, so I won't be able to finish constructing the bridge in time... What am I going to do?

Dora: That's not a problem! Boots and I can lend a helping hand, while you can go eat some of our delicious papayas.

Boots: Yes, well I think we have enough time to finish constructing the Royal Bridge before the Queen's Paddlewheel gets here. Give us the measurements, and we can finish the bridge in no time.

Construction Worker: Oh, thank you! The Royal Bridge must have a curved arch support that is 10 metres high and 16 metres wide. Well, I'm off then. Good day!

The construction worker took the papayas and walked down Hustleberry Lane.

Meanwhile...

Boots: Hey, Dora! We forgot to ask the construction worker what shape—a semi-circle, a semi-ellipse, a parabola, or a branch of a hyperbola—would give the best height available for the paddle steamer to pass safely beneath the bridge.

Dora: I guess the best height would have to be the shape that would give the maximum height possible, but which shape is it?

Dora and Boots are now faced with a problem. Help Dora and Boots solve the problem by answering the questions below.

QUESTIONS

a) The origin of the coordinate system has to be at the extreme left edge of the curved support. What is the equation of the curve in general form if the Royal Bridge is to be constructed in the shape of:

• a semi-circle?
• a semi-ellipse?
• a parabola?
• a branch of a hyperbola, where the length of the semi-transverse axis is 4 metres?

i. Semi-circle

Image 2.1

The equation of a circle in standard form is given, but only the top half of the circle will be drawn as part of the graph because the x-axis represents the ground. The bottom half of the bridge won't be built nor will the bridge be built underwater.

What We Know

• A point on the circle must be the origin of the coordinate system with the coordinates of (0, 0).
  
• Because the bridge has a maximum width of 16 metres, there is a point of intersection between the x-axis and the semi-circle with the coordinates (16, 0).
  
• The midpoint of these two coordinates is the centre of the circle with coordinates (8, 0).
  
• The radius should be 8 metres in length.
  
• Because the bridge has a maximum height of 10 metres, the coordinates of the maximum point on a circle is (8, 10).
  

Boots: Heeeey, wait a minute... These measurements don't make sense! If the radius of the circle along the x-axis is 8, then the distance between the centre of the circle to the maximum point on the circle must also be 8, not 10. Therefore, a semi-circle bridge with measurements of 10 metres as height and 16 metres as width is impossible.

You are right, Boots! I was just testing you.

ii. Semi-Ellipse

Image 2.2

The equation of a vertical ellipse in standard form is given, but only the top half of the ellipse will be drawn as part of the graph (making it a semi-ellipse) because the x-axis represents the ground. The bottom half of the bridge won't be built nor will the bridge be built underwater.

What We Know

• A point on the semi-ellipse must be the origin of the coordinate system with the coordinates of (0, 0).
  
• Because the bridge has a maximum width of 16 metres, there is a point of intersection between the x-axis and the semi-ellipse with the coordinates (16, 0).
  
• The midpoint of these two coordinates is the centre of the semi-ellipse with coordinates (8, 0).
  
• The semiminor axis, b, is 8 metres in length.
  
• Because the bridge has a maximum height of 10 metres, the coordinates of the maximum point on a circle is (8, 10).
• The semimajor axis, a, is 10 metres in length.
  
• The coordinates (x, y) represent any point on the semi-ellipse.
• The coordinates (h, k) represent the centre of the semi-ellipse.

Plug in these numbers into the equation, and an equation for the semi-ellipse is made. See Image 2.2.

iii. Parabola

Image 2.3

The equation of a vertical parabola in standard form is given, but only the parabola that is 10 metres above the ground will be drawn as part of the graph because the x-axis represents the ground. The bridge will not extend underwater nor will the bridge extend underground.

What We Know

• A point on the parabola must be the origin of the coordinate system with the coordinates of (0, 0). This is one of the parabola's roots.
  
• Because the bridge has a maximum width of 16 metres, there is a point of intersection between the x-axis and the parabola with the coordinates (16, 0). This is one of the parabola's roots.
  
• The midpoint of these two coordinates is found along the axis of symmetry (has the same x-coordinate as the vertex of the parabola) with coordinates (8, 0).
  
• The distance between the midpoint of the two ends of the bridge to one of either root is 8 metres in length.
  
• Because the bridge has a maximum height of 10 metres, the coordinates of the vertex is (8, 10).
• The distance between the midpoint of the two roots to the vertex is 10 metres in length.
• The coordinates (x, y) represent any point on the parabola.
• The coordinates (h, k) represent the vertex of the parabola.

Plug in these numbers into the equation, determine the distance between the focal point to the vertex by solving for p, and an equation for the parabola is made. See Image 2.3.

iv. Hyperbola

Image 2.4

The equation of a vertical hyperbola in standard form is given, but only the lower branch of the hyperbola that is 10 metres above the ground will be drawn as part of the graph because the x-axis represents the ground. The bridge will not extend underwater nor will the bridge extend underground nor will the bridge open up and hang suspended in mid-air.

What We Know

• A point on the hyperbola must be the origin of the coordinate system with the coordinates of (0, 0).
  
• Because the bridge has a maximum width of 16 metres, there is a point of intersection between the x-axis and the hyperbola with the coordinates (16, 0).
  
• The midpoint of these two coordinates is has coordinates (8, 0).
  
• The distance between the midpoint of the two ends of the bridge to one of either end of the bridge is 8 metres in length.
  
• Because the bridge has a maximum height of 10 metres, the coordinates of the vertex is (8, 10).
• The distance between the midpoint of the two ends of the bridge to the vertex is 10 metres in length.
• Because the length of the semitransverse axis, a, is 4 metres, the coordinates of the centre of the hyperbola is (8, 14).
  
• The coordinates (x, y) represent any point on the hyperbola.
• The coordinates (h, k) represent the centre of the hyperbola.

Plug in these numbers into the equation, determine the length of the semiconjugate axis by solving for b, and an equation for the hyperbola is made. See Image 2.3.

b) The Queen's Paddlewheel is a paddle steamer owned by the queen. She boards onto the paddle steamer on her voyage to Prince Livingston's Castle located near the other end of the river where the Royal Bridge is being constructed. The paddle steamer is measured to be 8 metres high above the water and 10 metres wide. Which of the four segments of the conic shapes—a semi-circle, a semi-ellipse, a parabola, a branch of a hyperbola—in a) would allow the paddle steamer to pass safely beneath the bridge, thus ensuring the safety of the queen?

Image 2.5

The width of the Royal Bridge is 16 metres while the height of the Royal Bridge is 10 metres.

The width of the Queen's Paddlewheel is 8 metres for height and 10 metres for width.

Dora and Boots wants to know which structure would give enough space for the paddle steamer to travel beneath the bridge. Because the width, x, of the paddle steamer is 10 metres, the height, y, of the paddle steamer must not be 8+ metres.

Plug in the numbers to where x is in the equation to get y. Reject all negative y-values because the boat can't have a negative height; the boat isn't underwater.

If the bridge were to have an elliptical shape, the height of the paddle steam can have a height up to sqrt(375/4) = 9.68 metres. The clearance is 1.68 metres (9.68 - 8 = 1.68). Thus, the paddle steamer won't collide into the bridge, and the queen is safe.

If the Royal Bridge were to have a parabolic shape, the height of the Queen's Paddlewheel can have a height up to 8 metres; the clearance is 0 metres (8 - 8 = 0). Thus, the paddle steamer will collide into the bridge, and the queen may drown.

If the Royal Bridge were to have a hyperbolic shape, the height of the paddle steam can have a height up to 8 metres; the clearance is 0 metres (8 - 8 = 0). Thus, the paddle steamer will collide into the bridge, and the queen may drown.

In conclusion, the best choice for the shape of the bridge is to construct the bridge in the shape of a semi-ellipse.

Happy Ending

After a hard day's work of homework, a mentally stimulating game of Go Fish, and an adventure to all sorts of places, they realize that math can be found anywhere, as long as we open our eyes to the math around us.

And they all lived happily ever after and ate papayas--they even shared some with Swiper.

THE END.